ANÁLISIS DE REGRESIÓN POISSON - EJEMPLO

Se realizó un estudio sobre el número de fallecidos por cáncer de pulmón en una determinada población clasificada por las variables Sexo y Edad. Los resultados obtenidos fueron los siguientes:

en donde se ha recogido, también, la Tasa de fallecimiento  r  para cada grupo, considerada como el cociente entre la población y el número de fallecidos.

Expresar la Tasa de Fallecimiento, en función de las covariables Sexo y Edad mediante un Modelo de Regresión Poisson de la forma

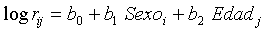
Comentarios:

           Mediante un Aálisis de Regresión Poisson se concluye que ambas covariables son significativas y, como las dos son de tipo cualitativo, el modelo ajustado dependerá de tantas covariables indicadores como clases tenga la covariable, menos una; es decir, que el Modelo de Regresión Poisson estimado es,

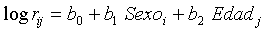
lo que lleva a estimar que, por ejemplo, para los Hombres, entre 50 y 70 Años, es de esperar un logaritmo para la Tasa de Fallecimiento igual a

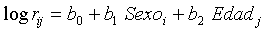
o lo que es lo mismo, despejando de la ecuación anterior, una Tasa de Fallecimiento esperada igual a

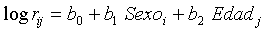
por lo que, en una población, semejante a la muestreada, de 3000 Hombres entre 50 y 70 Años,  cabría esperar  3000 · 0’096 =  288  fallecimientos. (Y esto, suponiendo que en cada celdilla, combinación de dos valores de cada variable, se observa una distribución Poisson.)